finden
Quadratic Curve 二次曲線説明器 summer
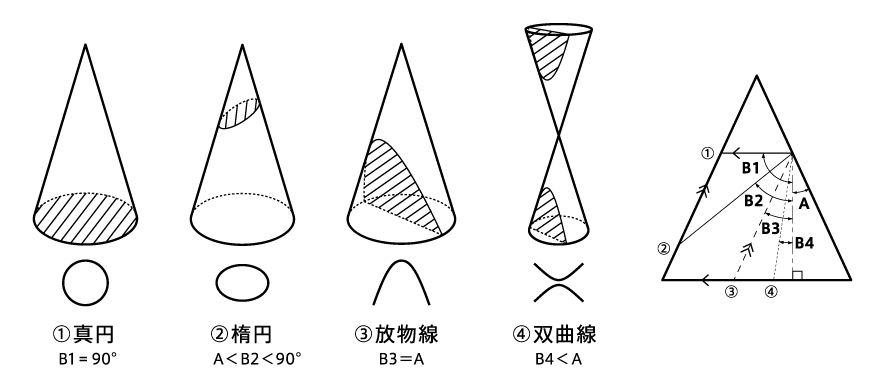
円錐をある条件で切断すると、その切断面が
「真円」「楕円」「放物線」「双曲線」となることをあらわしている模型です。
かつては中等・高等教育の現場において用いられていました。この模型も4つの数学的な曲線~二次曲線~を含んでいます。
二次曲線説明器 summer は 南の島の夏空をイメージした濃い青を配色しました。
寸法:φ120×200(mm)
重量:約460(g)
材質:木製 ウレタン樹脂塗装 ネオジム磁石埋込み 化粧箱入り
木製のため傷つきやすくなっています。特に端部は欠損しやすいのでお取り扱いにはご注意ください。
納品まで2週間程度頂いております。
ご使用過程における損傷(塗装の剥がれ、傷)については、可能な限り実費にて補修をさせていただきます。弊社宛お問い合わせください。

暮らしの中に隠れている数学の美しさに光をあて
心を豊かにするモノたちのブランチです
加藤数物製作所で製造していた数理模型たちを
現代的にアレンジしたフラッグシップ商品群です

二次曲線説明器は、円錐曲線を表現した模型です。 円錐曲線とは円錐を平面で切ったときに切り口に現れる楕円(ellipse)放物線(parabola)双曲線(hyperbola)の3種類の曲線のことです。
円錐曲線は、古代ギリシャ時代に発見、考え出されたもので、数々の研究により円錐表面と平面との関係よりいろいろな性質が明らかにされました。
17世紀ころには、さまざまな科学者によって宇宙の動きと関係していることがわかってきました。 ケプラーは太陽系の惑星が太陽を焦点の一つとする楕円軌道を回っていることを、ガリレオは物を投げたときに描く曲線がこの放物線であることを明らかにしました。さらにニュートンは万有引力の法則などニュートン力学をまとめることで、天体の運動も物を投げるときの運動も円錐曲線があてはめられることを証明し、その後パスカルやデカルトによって数学的な表現がなされ、二次曲線としての研究が進みました。
このシンプルな円錐で表現される曲線が、私達のいる地球を含めた宇宙の惑星が今の瞬間も進んでいる軌道であったり、ボールが飛んでいる軌跡であったり、自分たちの身近に接していた曲線であることは、知的な喜びを与えてくれます。